Mini Project: Monte Carlo Methods¶
In this notebook, you will write your own implementations of many Monte Carlo (MC) algorithms.
While we have provided some starter code, you are welcome to erase these hints and write your code from scratch.
# in this cell the environment is loaded
import gym
env = gym.make('Blackjack-v0')
Each state is a 3-tuple of:
- the player's current sum $\in \{0, 1, \ldots, 31\}$,
- the dealer's face up card $\in \{1, \ldots, 10\}$, and
- whether or not the player has a usable ace (
no$=0$,yes$=1$).
The agent has two potential actions:
STICK = 0
HIT = 1Verify this by running the code cell below.
# first exploration of the environment
# the observation space is the space of states
print("the states:", env.observation_space)
print("the actions:", env.action_space)
print("number of actions:", env.action_space.n)
Execute the code cell below to play Blackjack with a random policy.
(The code currently plays Blackjack three times - feel free to change this number, or to run the cell multiple times. The cell is designed for you to get some experience with the output that is returned as the agent interacts with the environment.)
# looking at episodes
# calculating three episodes
for i_episode in range(3):
# with the reset method you get the environment back to the starting point
state = env.reset()
# until the episode ends
while True:
# print the actual state
print(state)
# get the next action with the environments action_space.sample() method
action = env.action_space.sample()
# with the action we can get the next step
# the step delivers a next state, a reward, an indicator whether the episode ends
# and some info that is not needed here
state, reward, done, info = env.step(action)
# if the episode ends
if done:
# print the final reward
print('End game! Reward: ', reward)
# judge on the outcome of the episode
print('You won :)\n') if reward > 0 else print('You lost :(\n')
# break the step loop for the episode
break
Part 1: MC Prediction: State Values¶
In this section, you will write your own implementation of MC prediction (for estimating the state-value function).
We will begin by investigating a policy where the player always sticks if the sum of her cards exceeds 18. The function generate_episode_from_limit samples an episode using this policy.
The function accepts as input:
bj_env: This is an instance of OpenAI Gym's Blackjack environment.
It returns as output:
episode: This is a list of (state, action, reward) tuples (of tuples) and corresponds to $(S_0, A_0, R_1, \ldots, S_{T-1}, A_{T-1}, R_{T})$, where $T$ is the final time step. In particular,episode[i]returns $(S_i, A_i, R_{i+1})$, andepisode[i][0],episode[i][1], andepisode[i][2]return $S_i$, $A_i$, and $R_{i+1}$, respectively.
# generates episodes under a deterministic policy of a limit on the hand cards
def generate_episode_from_limit(bj_env):
"""generates episodes for a policy of setting a limit:
- the policy chooses 'hit' if the own hand is less then 18, otherwise it chooses 'stick'
"""
episode = []
state = bj_env.reset()
while True:
# get action from the policy
action = 0 if state[0] > 18 else 1
next_state, reward, done, info = bj_env.step(action)
episode.append((state, action, reward))
state = next_state
if done:
break
return episode
Execute the code cell below to play Blackjack with the policy.
(The code currently plays Blackjack three times - feel free to change this number, or to run the cell multiple times. The cell is designed for you to gain some familiarity with the output of the generate_episode_from_limit function.)
# This cell explore how returns are computed for one episode
# numpy is needed for the array operations
import numpy as np
# first generate the episode
episode = generate_episode_from_limit(env)
# the episode consists of tuples of the structure (state, action, reward)
print("episode:", episode)
# collect states, actions and rewards into seperate lists
# the list are connected by the index which is the step in the episode
states, actions, rewards = zip(*episode)
# this results in zip objects that can be turned into lists
print("\n-->print the lists associated with the episode:")
print("states:", list(states))
print("actions:", list(actions))
print("rewards:", list(rewards))
# for discounting we need discount factors
gamma = 0.9
discounts = np.array([gamma**i for i in range(len(rewards)+1)])
print("discount factors:", discounts)
# now we go through the steps to collect the returns
print("\n-->now going through the states of an episode:")
for i, state in enumerate(states):
print("step and state:", i, state)
print("the rewards are", rewards[i:]) # get all rewards from here on
# get as many discount factors as rewards
len_rewards = len(rewards[i:])
print("the discount factors are:", discounts[:len_rewards])
# we get
for i in range(3):
print(generate_episode_from_limit(env))
Now, you are ready to write your own implementation of MC prediction. Feel free to implement either first-visit or every-visit MC prediction; in the case of the Blackjack environment, the techniques are equivalent.
Your algorithm has three arguments:
env: This is an instance of an OpenAI Gym environment.num_episodes: This is the number of episodes that are generated through agent-environment interaction.generate_episode: This is a function that returns an episode of interaction.gamma: This is the discount rate. It must be a value between 0 and 1, inclusive (default value:1).
The algorithm returns as output:
V: This is a dictionary whereV[s]is the estimated value of states. For example, if your code returns the following output:
then the value of state{(4, 7, False): -0.38775510204081631, (18, 6, False): -0.58434296365330851, (13, 2, False): -0.43409090909090908, (6, 7, False): -0.3783783783783784, ...(4, 7, False)was estimated to be-0.38775510204081631.
If you are unfamiliar with how to use defaultdict in Python, you are encouraged to check out this source.
from collections import defaultdict
import numpy as np
import sys
def mc_prediction_v(env, num_episodes, generate_episode, gamma=1.0):
"""this function approximates the state function V by going through a fixed number
of episodes. For each time the state appears in an episode the cumulated return
is stored. The state function for that state is assigned the mean of the cumulated
returns for all episodes.
There are two approaches:
- collect every visit to a state on an episode
- collect only first visits
In this function every visit is collected, but in the case of Black Jack that does not
make a difference since states just occur once in each episode
"""
# initialize the returns for each state as an empty list
returns = defaultdict(list)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# generate the episode, see above
episode = generate_episode(env)
# the states, actions and rewards are turned into seperate lists by this statement
# the index connect them as the step
states, actions, rewards = zip(*episode)
# get simple chain of discount factors of gamma**i's
discounts = np.array([gamma**i for i in range(len(rewards)+1)])
for i, state in enumerate(states):
# for every state that appears in the episode collect the discounted returns
# i is the step in the episode and state is the state encountered at step i
# collect the rewards from step i onwards to the end of the episode
rewards_chain = rewards[i:]
# get as many discount factors as there are rewards
discount_chain = discounts[:len(rewards_chain)]
# compute the discounted expected reward
# as the sum of rewards times discount factors
sum_discounted_rewards = sum(rewards_chain * discount_chain)
# append the expected reward for to the returns list for that state
returns[state].append(sum_discounted_rewards)
# after all returns have been collected the state function is computed as the mean
# return for every state
V = {state: np.mean(reward_list) for state, reward_list in returns.items()}
# the state function is returned
return V
Use the cell below to calculate and plot the state-value function estimate. (The code for plotting the value function has been borrowed from this source and slightly adapted.)
To check the accuracy of your implementation, compare the plot below to the corresponding plot in the solutions notebook Monte_Carlo_Solution.ipynb.
from plot_utils import plot_blackjack_values
# run the iteration with the given policy and
# obtain the value function
V = mc_prediction_v(env, 500000, generate_episode_from_limit)
# plot the value function
plot_blackjack_values(V)
Part 2: MC Prediction: Action Values¶
In this section, you will write your own implementation of MC prediction (for estimating the action-value function).
We will begin by investigating a policy where the player almost always sticks if the sum of her cards exceeds 18. In particular, she selects action STICK with 80% probability if the sum is greater than 18; and, if the sum is 18 or below, she selects action HIT with 80% probability. The function generate_episode_from_limit_stochastic samples an episode using this policy.
The function accepts as input:
bj_env: This is an instance of OpenAI Gym's Blackjack environment.
It returns as output:
episode: This is a list of (state, action, reward) tuples (of tuples) and corresponds to $(S_0, A_0, R_1, \ldots, S_{T-1}, A_{T-1}, R_{T})$, where $T$ is the final time step. In particular,episode[i]returns $(S_i, A_i, R_{i+1})$, andepisode[i][0],episode[i][1], andepisode[i][2]return $S_i$, $A_i$, and $R_{i+1}$, respectively.
def generate_episode_from_limit_stochastic(bj_env):
episode = []
state = bj_env.reset()
while True:
probs = [0.8, 0.2] if state[0] > 18 else [0.2, 0.8]
action = np.random.choice(np.arange(2), p=probs)
next_state, reward, done, info = bj_env.step(action)
episode.append((state, action, reward))
state = next_state
if done:
break
return episode
# the episodes are the same as before, just the way we created them changed54
episode = generate_episode_from_limit_stochastic(env)
print(episode)
Now, you are ready to write your own implementation of MC prediction. Feel free to implement either first-visit or every-visit MC prediction; in the case of the Blackjack environment, the techniques are equivalent.
Your algorithm has three arguments:
env: This is an instance of an OpenAI Gym environment.num_episodes: This is the number of episodes that are generated through agent-environment interaction.generate_episode: This is a function that returns an episode of interaction.gamma: This is the discount rate. It must be a value between 0 and 1, inclusive (default value:1).
The algorithm returns as output:
Q: This is a dictionary (of one-dimensional arrays) whereQ[s][a]is the estimated action value corresponding to statesand actiona.
def mc_prediction_q(env, num_episodes, generate_episode, gamma=1.0):
"""this is for counting every visit"""
# initialize empty dictionaries with stochastic functions, that map both actions to 0
# returns are collected in lists
returns = defaultdict(list)
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# collect the rewards for all episodes: use all visits
episode = generate_episode(env)
states, actions, rewards = zip(*episode)
discounts = np.array([gamma**i for i in range(len(rewards)+1)])
# now we need to compute the returns for all state action pairs:
for i, state in enumerate(states):
# action is the action taken
action = actions[i]
rewards_chain = rewards[i:]
discount_chain = discounts[:len(rewards_chain)]
sum_discounted_rewards = sum(rewards_chain * discount_chain)
returns[(state, action)].append(sum_discounted_rewards)
Q = defaultdict(lambda: np.zeros(env.action_space.n))
for state_action_pair, expected_rewards in returns.items():
action = state_action_pair[1]
state = state_action_pair[0]
Q[state][action] = np.mean(expected_rewards)
return Q
Use the cell below to obtain the action-value function estimate $Q$. We have also plotted the corresponding state-value function.
To check the accuracy of your implementation, compare the plot below to the corresponding plot in the solutions notebook Monte_Carlo_Solution.ipynb.
# obtain the action-value function
Q = mc_prediction_q(env, 500000, generate_episode_from_limit_stochastic)
# obtain the state-value function
V_to_plot = dict((k,(k[0]>18)*(np.dot([0.8, 0.2],v)) + (k[0]<=18)*(np.dot([0.2, 0.8],v))) \
for k, v in Q.items())
# plot the state-value function
plot_blackjack_values(V_to_plot)
Part 3: MC Control: GLIE¶
In this section, you will write your own implementation of constant-$\alpha$ MC control.
Your algorithm has three arguments:
env: This is an instance of an OpenAI Gym environment.num_episodes: This is the number of episodes that are generated through agent-environment interaction.gamma: This is the discount rate. It must be a value between 0 and 1, inclusive (default value:1).
The algorithm returns as output:
Q: This is a dictionary (of one-dimensional arrays) whereQ[s][a]is the estimated action value corresponding to statesand actiona.policy: This is a dictionary wherepolicy[s]returns the action that the agent chooses after observing states.
(Feel free to define additional functions to help you to organize your code.)
def generate_epsilon_greedy_episode_from_q(env, epsilon, Q, nA):
episode = []
state = env.reset()
p_default_epsilon = epsilon / nA
p_default = 1 / nA
while True:
if state in Q:
probs = [p_default_epsilon] * nA
greedy_choice = np.argmax(Q[state])
probs[greedy_choice] = 1 - epsilon + (epsilon / nA)
else:
probs = [p_default] * nA
action = np.random.choice(np.arange(nA), p=probs)
next_state, reward, done, info = env.step(action)
episode.append((state, action, reward))
state = next_state
if done:
break
return episode
def mc_control_GLIE(env, num_episodes, gamma=1.0):
nA = env.action_space.n
# initialize empty dictionaries of arrays
Q = defaultdict(lambda: np.zeros(nA))
N = defaultdict(lambda: np.zeros(nA))
# loop over episodes
for i_episode in range(1, num_episodes+1):
epsilon = 1.0/((i_episode / 10000) + 1)
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
# collect the rewards for all episodes: use all visits
episode = generate_epsilon_greedy_episode_from_q(env, epsilon, Q, nA)
states, actions, rewards = zip(*episode)
discounts = np.array([gamma**i for i in range(len(rewards)+1)])
for i, state in enumerate(states):
action = actions[i]
old_Q = Q[state][action]
N[state][action] += 1
rewards_chain = rewards[i:]
discount_chain = discounts[:len(rewards_chain)]
sum_discounted_rewards = sum(rewards_chain * discount_chain)
Q[state][action] = old_Q + (sum_discounted_rewards - old_Q) / N[state][action]
# for state assign action
policy = dict((state, np.argmax(action)) for state, action in Q.items())
return policy, Q
Use the cell below to obtain the estimated optimal policy and action-value function.
# obtain the estimated optimal policy and action-value function
policy_glie, Q_glie = mc_control_GLIE(env, 500000)
Next, we plot the corresponding state-value function.
# obtain the state-value function
V_glie = dict((k,np.max(v)) for k, v in Q_glie.items())
# plot the state-value function
plot_blackjack_values(V_glie)
Finally, we visualize the policy that is estimated to be optimal.
from plot_utils import plot_policy
# plot the policy
plot_policy(policy_glie)
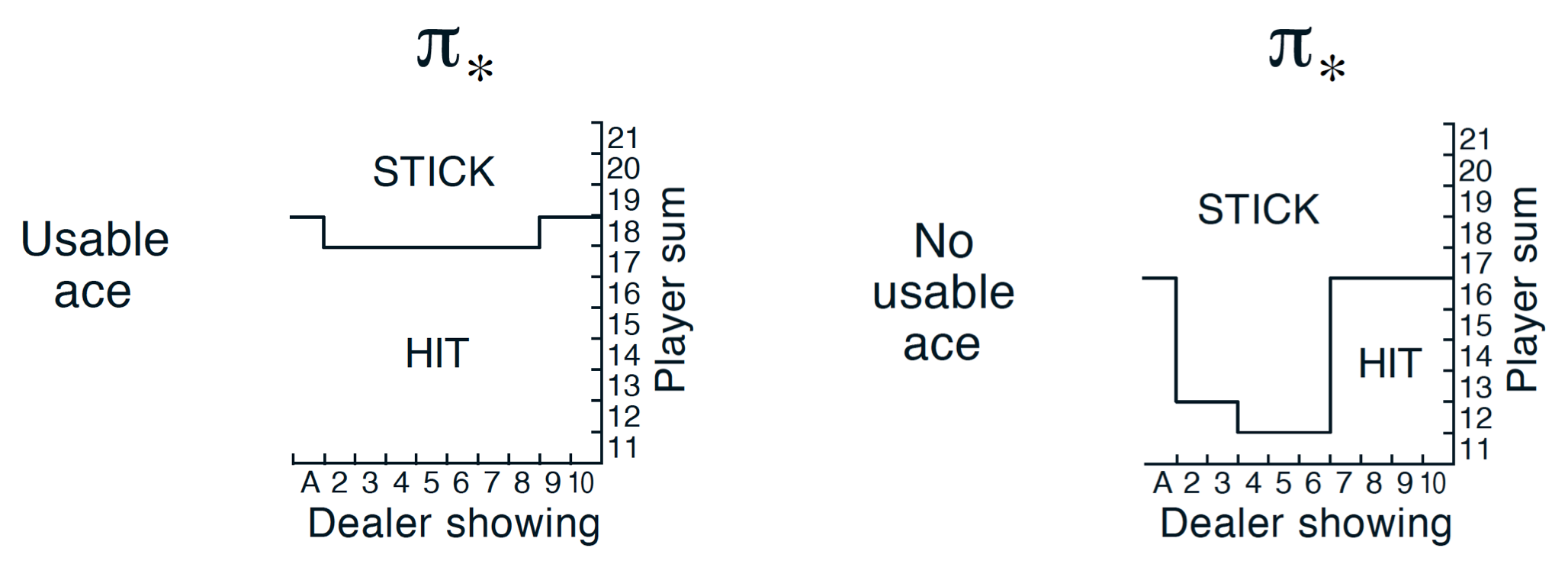
The true optimal policy $\pi_*$ can be found on page 82 of the textbook (and appears below). Compare your final estimate to the optimal policy - how close are you able to get? If you are not happy with the performance of your algorithm, take the time to tweak the decay rate of $\epsilon$ and/or run the algorithm for more episodes to attain better results.
Part 4: MC Control: Constant-$\alpha$¶
In this section, you will write your own implementation of constant-$\alpha$ MC control.
Your algorithm has four arguments:
env: This is an instance of an OpenAI Gym environment.num_episodes: This is the number of episodes that are generated through agent-environment interaction.alpha: This is the step-size parameter for the update step.gamma: This is the discount rate. It must be a value between 0 and 1, inclusive (default value:1).
The algorithm returns as output:
Q: This is a dictionary (of one-dimensional arrays) whereQ[s][a]is the estimated action value corresponding to statesand actiona.policy: This is a dictionary wherepolicy[s]returns the action that the agent chooses after observing states.
(Feel free to define additional functions to help you to organize your code.)
def mc_control_alpha(env, num_episodes, alpha, gamma=1.0):
nA = env.action_space.n
# initialize empty dictionary of arrays
Q = defaultdict(lambda: np.zeros(nA))
# loop over episodes
for i_episode in range(1, num_episodes+1):
# monitor progress
if i_episode % 1000 == 0:
print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
sys.stdout.flush()
epsilon = 1.0/((i_episode / 10000) + 1)
# collect the rewards for all episodes: use all visits
episode = generate_epsilon_greedy_episode_from_q(env, epsilon, Q, nA)
states, actions, rewards = zip(*episode)
discounts = np.array([gamma**i for i in range(len(rewards)+1)])
for i, state in enumerate(states):
action = actions[i]
old_Q = Q[state][action]
rewards_chain = rewards[i:]
discount_chain = discounts[:len(rewards_chain)]
sum_discounted_rewards = sum(rewards_chain * discount_chain)
Q[state][action] = old_Q + (sum_discounted_rewards - old_Q) * alpha
# for state assign action
policy = dict((state, np.argmax(action)) for state, action in Q.items())
return policy, Q
Use the cell below to obtain the estimated optimal policy and action-value function.
# obtain the estimated optimal policy and action-value function
policy_alpha, Q_alpha = mc_control_alpha(env, 500000, 0.008)
Next, we plot the corresponding state-value function.
# obtain the state-value function
V_alpha = dict((k,np.max(v)) for k, v in Q_alpha.items())
# plot the state-value function
plot_blackjack_values(V_alpha)
Finally, we visualize the policy that is estimated to be optimal.
# plot the policy
plot_policy(policy_alpha)
The true optimal policy $\pi_*$ can be found on page 82 of the textbook (and appears below). Compare your final estimate to the optimal policy - how close are you able to get? If you are not happy with the performance of your algorithm, take the time to tweak the decay rate of $\epsilon$, change the value of $\alpha$, and/or run the algorithm for more episodes to attain better results.
